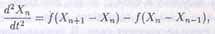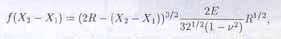Источник 122

Даниленко В.А., Белинский И.В., Венгрович Д.Б., Гржибовский В.В., Лемешко В.А.

Институт геофизики им.С.И.Субботина НАН Украины, г.Киев

Особенности волновых процессов в геофизических средах при учете их структуры

- Доклады НАН Украины, 1996, N 12. - с.124-129

Даниленко В.А., Бєлiнський I.В., Венгрович Д.Б., Гржибовський В.В., Лемешко В.А.

Iнститут геофiзики iм.С.I.Субботiна НАН України, м.Київ

Особливостi хвильових процесiв у геофiзичних середовищах при врахуваннi їх структури

- Доповiдi НАН України, 1996, N 12. - с.124-129

Results of experimental and theoretical researches of wave processes in discrete media are given. The existence of stationary perturbation of soliton-like type for a one-dimensional chain of balls is established. Distinctive space length of a soliton is amplitude-independent and occupies four balls. The pulsing of a soliton amplitude along the chain is experimentally found for the first time.

Перевод с украинского Шестопалова А.В.

Континуальные представления о геофизической среде дают возможность достигнуть успехов при решении многих задач геофизики (сейсморазведки, сейсмологии). Однако в последние годы получены геофизические данные, которые показывают, что вопросы связанные с описанием деформирования верхних твердых оболочек Земли под действием тектонических сил, вопросы интерпретации сейсмических данных, а так же процессов, которые сопровождают подготовку землетрясений, не возможно решить без учета структурных особенностей геофизической среды [1, 2]. Так распределение потока сейсмической энергии от землетрясений разного класса описывается законом, который свидетельствует о иерархаичной дискретной структуре твердой оболочки Земли [1, 2].

То есть, возникает проблема исследования волновых процессов в дискретных средах и построения математической модели, которая адекватно описывала бы процессы деформирования геофизической среды и структуры. При построении математической модели такой среды возникает ряд трудностей принципиального характера. Учет структуры среды не позволяет использовать ра'звитый к настоящему времени математический аппарат континуальной механики и термодинамики сплошной среды, при использовании которого решено ряд практических задач геофизики.

При экспериментальном исследовании волновых процессов в геофизической среде с учетом ее дискретной структуры необходимо решить ряд принципиальных вопросов методического характера, таких как проблема измерения деформаций, массовых скоростей в неравновесной дискретной среде, проблема обработки и интерпретации полученных результатов.

В данной работе приведены результаты экспериментальных и теоретических исследований распространения нелинейных импульсных возбуждений в дискретной среде. Дискретная среда моделировалась цепью стальных шаров. Акустические характеристики такой среды близки к акустическим характеристикам дискретной среды, состоящей из гранул (блоков) интрузивных пород Украинского щита.

При экспериментальном исследовании изучено распространение возбуждений по цепи из 24 стальных шаров диаметром 41,25 мм. Возбуждение в цепи вызывалось ударом такого же шара, что и шар в цепи. Скорость шара изменялась от 0,16 до 2,8 м/с. Датчик-шар, который фиксирует возбуждение в цепи, однозначно есть структурным элементом цепи и представляет собой
[с.124]
склеянный эпоксидным клеем предварительно разрезанный стальной шар. В центральной части диаметральной плоскости разрезанного шара размещался чувствительный элемент. Сигнал от датчика через согласующий усилитель подавался на осциллограф, от куда информация подавалась на компьютер. Датчик-шар регистрирует силу, которая действует на контакте двух шаров при их взаимодействии. Погрешность от расположения в цепи шаров датчика-шара не превышает 2%.

Использование датчика, который одновременно является структурным элементом среды, дает возможность детально проанализировать трансформацию возбуждения, которое распространяется в дискретной среде.

Эволюцию возбуждения, которое распространяется по горизонтальной цепи 24 стальных шаров при ударе со скоростью 0,7 м/с проиллюстрировано на рис. 1. Для первых двух и двух последних шаров в цепи амплитудно-временные параметры возбуждения при ударе значительно отличаются от аналогичных параметров шаров от 3 до 22.

Рис. 1. Эволюция возбуждения в горизонтальной цепи шаров

То есть, возбуждение уже после 2-го шара стабилизируется и таким сохраняется вдоль всей цепи, за исключением двух последних шаров. Осредненные параметры стационарных возбуждений, которые распространяются по цепи 24 шаров, приведены в табл. 1,

Таблица 1. [с.126]

где u - скорость шара, который ударяет;
      c^e_o - скорость распространения возбуждения;
      t и l/d - соответственно временная и относительная пространственная полуширина возбуждения;
      F_m - максимальное значение силы.

В скобках приведены среднеквадратичные отклонения от средних значений стационарных возбуждений. Следует отметить, что амплитудно-временные параметры для шаров с 3 по 22, не являются постоянными. Максимальное значение силы изменяется вдоль цепи шаров почти периодично, как это показано на рис. 2. Период этих колебаний составляет 6 шаров, а максимальное отклонение значения силы от среднего - около 3-4%.
[c.125]

Рис. 2. Зависимость временно'й полуширины (1) и максимальной силы (2) от положения датчика-шара при ударе по цепи шаров со скоростью 0,7 м/с

При численном моделировании изучено распространение возбуждения в цепи из 300 стальных шаров, параметры которых описаны в тексте согласно эксперимента. Моделируется одновременный удар крайними шарами по очереди шаров цепи со скоростью [u] = u_o. Распространение возбуждения описывается уравнением [3]

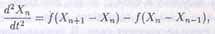
(1)

где X_n - смещение n-го шара из положения равновесия.

Так как задача симетрична относительно центра цепи, то достаточно рассмотреть половину из набора шаров при граничных условиях: для центрального шара: X = 0 - жесткая граница; для крайнего шара: N = 150, f ( X₁₅₁ - X₁₅₀ ) = 0; а так же для начальных условий

t = 0, u ( X_n ) = 0, n = 1, ..., 149, u ( X₁₅₀ ) = - u_o.

Рассмотрим уравнение (1) для случая взаимодействия стальных шаров радиуса R по закону Герца [4], когда его правая часть состоит из сил взаимодействия соседей вида

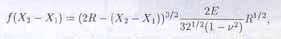
(2)

где E, n - соответственно модуль Юнга и коэффициент Пуассона стали.

Следует отметить, что наряду с явной нелинейностью силы (2) в правую часть уравнения (1) неявно входит нелинейность другого качества, что обусловленно необходимостью учитывать отсутствие взаимодействия шаров, центры которых разошлись на расстояние, большее 2R. Таким образом, класс решений задачи должен учитывать возможность такой разрывности в уравнении (1). В связи с этим автор работ [5, 6] рассматривает сжатую цепь, когда физически обеспечивается невозможность расхождения соседних шаров, однако это не снимает с математической точки зрения вопрос о классе функций, в котором ведется поиск решения. По этому мы считаем некорректным математическим моделированием распространения возмущения в средах со структурой (таких, как геофизическая среда, цепи шаров) на основании континуальных уравнений, как это сделано в работах, где интерпретируется возбуждение от землетрясений [7] и возбуждение в цепи шаров [5, 6]. Именно по этому мы остановились на прямом численном моделировании распространения возбуждений в цепи шаров на базе уравнений (1), (2).

Система дифференциальных уравнений решена программой на базе метода экстраполяции с переменным шагом и порядком на компьютере класса SPARC. Локальная ошибка выдерживалась близкой 10^-30.

Рис. 3. Зависимость скорости центров масс в половине цепи из n = 50 шаров от времени t после одновременного удара краями шаров с начальной u = 100 см/с

Зависимость скорости шаров половины цепи от времени приведено на рис. 3. Наблюдается распространение локализованной волны, которая в определенный момент времени сталкивается с такой же встречной волной. Следует отметить, что рассеивание волн не является чисто упругим, поэтому в строгом понимании наблюдается солитоноподобная волна - при взаимодействии генерируются новые

[с.127]

"солитоны" меньшей амплитуды.

Изолинии скорости шаров для начальной стадии возникновения волны изображены на рис. 4. Можно утверждать, что волна быстро формируется и в целом хорошо сохраняет свою форму в процессе движения, локализуясь на четырех соседних шарах. Заметна небольшая пульсация амплитуды и ширины импульса.

Рис. 4. Изолинии u(x, t) для скорости удара u = 150 см/с (n = 150, t = 0)

Для классификации результатов по характеру возбуждений, полученных экспериментально, сравним их с результатами численного моделирования (рис. 3, 4, табл. 1).

Экспериментальные значения временно'й полуширины (t) возбуждения описываются эмпирической зависимостью t = 123u^-0,19, а его пространственная полуширина (l/d) не зависит от скорости удара и составляет l/d = 2,05 ± 0,4%. То есть, волновое возмущение формируется в цепи шаров четырьмя шарами, что совпадает с результатами численного моделирования. Экспериментальные значения скорости распространения возмущения по цепи шаров, вызванного ударом, описывается эмпирической зависимостью c^e_o = 694u^0,19, что достаточно точно совпадает с теоретическими расчетами c^t_o = 706u^0,20.

Таким образом, анализ приведенных результатов дает основание утверждать, что волновые возбуждения, которые наблюдаются в эксперименте, являются солитоноподобными волнами. Впервые экспериментально исследована эволюция параметров возмущения, распространяющегося вдоль всей

[c.128]

длины дискретной среды (цепи шаров) во время удара без нарушения свойств ее элементов. При этом убедительно показано существование стационарного возбуждения солитоноподобного типа для одноразмерной цепи шаров. Характерный пространственный размер солитона не зависит от амплитуды возбуждения и равняется четырем шарам. Впервые экспериментально установлена пульсация амплитуты солитона по длине цепи.

Сравнение с численным моделированием показывает удовлетворительное совпадение результатов, что указывает на возможность дальнейшего исследования с таким подходом явлений распространения возмущений в средах со структурой (таких, как геофизическая среда, цепи шаров и другие дискретные среды).

Работа частично поддержана Международным научным фондом Дж.Сороса (International Science Foundation) (гранты N UAE000 ma N UAE200).

Авторы выражают благодарность коллегам с группы Осадочной геофизики Свободного университета (г.Амстердам) за содействие в проведении расчетов.

1. Родионов В.Н., Сизов И.А., Цветков В.М. Основы геомеханики. - М.: Недра, 1986. - 301с.

2. Садовский М.А., Болховитинов Л.Г., Писаренко Г.П. Деформируемость геофизической среды и сейсмический процесс. - М.: Наука, 1987. - 100с.

3. Fermi E., Pasta J.R., Ulam S.M. Studies on non-linear problems // Collected works of Enrico Fermi. - Chicago: University of Chicago Press, 1965. - V.2. - P.978-988.

4. Ландау Л.Д., Лифшиц Е.М. Механика сплошных сред. - М., 1953. - 788с.

5. Нестеренко В.Ф. Распространение нелинейных импульсов сжатия в зернистых средах // ПМТФ, 1983, N 5. - с.136-148.

6. Нестеренко В.Ф. Импульсное нагружение гетерогенных материалов. - Новосибирск, 1992. - 200с.